The Zenith of Ancient Indian Science
In the heart of India’s intellectual history, amidst the temples and flourishing centers of learning of the 12th century, arose a scholar whose brilliance would shine for centuries: Bhāskara II, often revered as Bhaskarāchārya (“Bhāskara the Teacher”). He wasn’t just another Indian mathematician and astronomer; he was the lineal successor to giants like Aryabhatta and Brahmagupta, and arguably the greatest mathematician of medieval India.
His story matters because he didn’t just compile old knowledge; he perfected it and, astonishingly, pioneered concepts like the foundations of differential calculus centuries before Europe’s scientific revolution. Bhaskara’s major scientific achievements—from his systematic use of the decimal system to his advanced solutions for indeterminate equations—make him an enduring inspiration for students and a testament to the sophistication of Indian science. 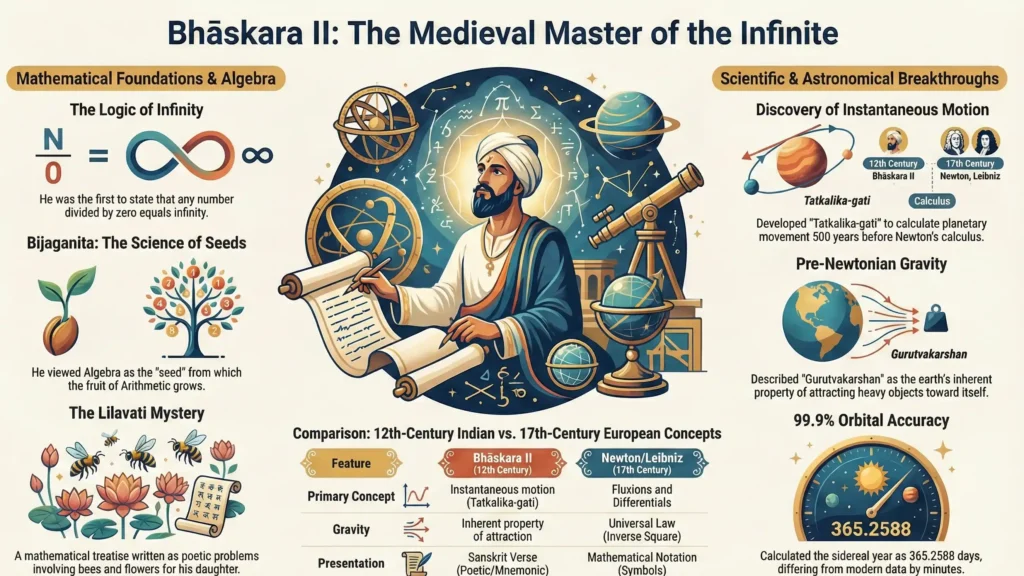His masterpiece, the Siddhānta Shiromaṇi (Crown of Treatises), remains a dazzling jewel in the crown of global intellectual history.
Early Life and Education: A Heritage of Heavenly Knowledge
Bhāskara II was born in 1114 CE in a village called Vijjadavida (near modern-day Bijapur, Karnataka). He belonged to a highly respected Deshastha Brahmin family with a long tradition of scholars and spiritual teachers. Knowledge wasn’t just a pursuit in his family; it was a hereditary duty.
His father, Maheswara, was a renowned astrologer and mathematician who served as his son’s first and perhaps most influential mentor. We can imagine young Bhāskara growing up surrounded by celestial charts, astronomical instruments, and the constant rhythm of intellectual discussion. His early education was intensely focused on the traditional Indian sciences (Jyotisha), which required mastery of Ganita (mathematics) for precise calculation of time, planetary movements, and religious calendars.
This familial environment ensured that Bhāskara inherited not only a vast library of knowledge but also the rigorous discipline required to challenge and advance it. He was building on a foundation that stretched back over a millennium, ready to take the next monumental leap.
Journey into Science: The Head of the Ujjain Observatory
Bhāskara II’s career path led him to the most prestigious mathematical centre of his time: the astronomical observatory at Ujjain (in modern-day Madhya Pradesh). Ujjain was the historical prime meridian for Indian astronomers and had been the workplace of mathematical giants like Varāhamihira and Brahmagupta. It was here, as the head of the observatory (Kulapati), that Bhāskara solidified his reputation and produced his most seminal works.
His entry into the field was marked by an exhaustive study of the existing Siddhanta texts. His genius lay in his ability to identify the gaps and errors in previous works, particularly those of Brahmagupta. He didn’t just want to repeat knowledge; he wanted to perfect it.
His masterpiece, the Siddhānta Śiromaṇi (Crown of Treatises), was completed in 1150 CE when he was just 36. This monumental text is divided into four main parts, two of which are dedicated to mathematics and two to astronomy:
* Līlāvatī (Arithmetic and Geometry)
* Bījagaṇita (Algebra)
* Grahagaṇita (Mathematics of the Planets)
* Golādhyāya (Mathematics of the Spheres)
The sheer scope and clarity of this work immediately positioned him as the foremost scholar of his age.
Major Achievements and Contributions: Foreshadowing Calculus
Bhāskara II’s contributions were revolutionary, pushing the boundaries of what was mathematically possible in the 12th century.
🧮 The Human Touch in Mathematics: Līlāvatī
The first part of his major work, the Līlāvatī, is the most famous, due to an endearing legend. It is said he wrote it for his daughter, Līlāvatī, to console her after a tragic event surrounding her marriage. The text is written in beautiful, inviting verse, posing mathematical problems as riddles to an intelligent young girl:
> “Oh Līlāvatī, intelligent girl, if you understand addition and subtraction, tell me the sum of the amounts 2, 5, 32, 193, 18, 10, and 100…”
>
This approach made complex arithmetic and geometry accessible and engaging, ensuring that his work was treasured and used as a textbook for centuries. Beyond the storytelling, the text systematically introduced the decimal number system, including the decimal point, to a wide audience.
➗ Solving the Unsolvable: Advanced Algebra
In Bījagaṇita, Bhāskara took algebra to unprecedented heights:
* Pell’s Equation: He provided a general, systematic solution for the indeterminate quadratic equation x^2 = 1 + py^2, famously known as Pell’s Equation in the West. His method, called the Chakravala (or “cyclic”) method, was an iterative algorithm that yielded the exact integer solution and was centuries ahead of European mathematicians. In fact, a specific problem posed by Pierre de Fermat in the 17th century was solved using a variant of Bhaskara’s method.
* Division by Zero and Infinity: He had a clearer grasp of the mathematical properties of zero than his predecessors. He clearly stated that the value of any number divided by zero (\frac{a}{0}) is infinity (ananta), which, though not perfectly aligned with modern definitions, showed a profound initial understanding of the concept of mathematical limits.
📈The Calculus Pioneer
Perhaps his most stunning scientific achievement lay in his astronomical treatises. While trying to accurately calculate the instantaneous speed and position of planets, Bhāskara developed principles that anticipated calculus:
* He noted that when a planet is at its farthest or nearest point to Earth, the change in its motion is instantaneously zero. This observation hinted at the concept of the derivative—finding the slope of a curve at a point—a central idea of differential calculus.
* He used the idea of infinitesimals and introduced the equivalent of Rolle’s Theorem, a cornerstone of mathematical analysis, to astronomical problems.
Challenges and Turning Points: The Tragic Muse
The greatest personal turning point in Bhāskara’s life is forever entwined with the Līlāvatī text, serving as a powerful, albeit legendary, emotional backdrop to his work.
The anecdote tells of Bhāskara, proficient in astrology, predicting that his beloved daughter Līlāvatī was fated to an unhappy marriage unless she was wed at a precise, auspicious moment. To measure this moment, he devised a precise water-clock (a ghati yantra)—a vessel with a small hole that would sink at the exact time. He warned Līlāvatī not to disturb the device. Tragically, in her curiosity, a pearl from her bridal dress accidentally fell into the vessel, blocking the hole and causing the auspicious moment to pass unnoticed. The marriage, conducted at the wrong time, ended in tragedy.
Devastated by his inability to thwart fate despite his scientific precision, Bhāskara promised his grieving daughter solace through knowledge. He vowed to write a book in her name, one that would make her immortal, saying, “A good name is a second life.” This legendary event transformed his grief into a powerful creative force, resulting in a mathematical text that was both rigorous and deeply humane, making it his most enduring and accessible work.
Legacy and Inspiration: The Eternal Teacher
Bhāskara II’s legacy is monumental. He represents the pinnacle of ancient Indian mathematics and his comprehensive works became the standard texts for centuries, influencing mathematical thought not only in India but also through translations that reached the Middle East.
His greatest impact is perhaps the inspiration for students he provides, both through his rigorous research and the poignant story of Līlāvatī:
* Blending Rigor with Empathy: The story of Līlāvatī teaches us that even the most complex subjects can be taught with kindness, clarity, and personal connection. Bhāskara elevated mathematics from a mere calculation tool into an art form.
* The Power of Anticipation: His work on the Chakravala method and early calculus principles demonstrates the boundless power of human intellect to foresee and solve problems that the world won’t formally recognize for hundreds of years. He encourages us to think beyond the immediate horizon.
Today, Bhāskara II stands as a shining example of a true Indian scientist—a genius who perfected the past, defined his present, and peered centuries into the future of mathematics.
Read More: https://curiousindian.in/bhaskara-i-c-600-c-680-ce/
