Pingala was an ancient Indian mathematician and linguist who lived between the 3rd and 2nd Century BCE. He is the first person in recorded history to describe a binary numeral system and the mathematical triangle now known as Pascal's Triangle. Through his work on Sanskrit prosody, the Chandaḥśāstra, he developed the Pingala Binary System, which laid the essential groundwork for combinatorics, probability, and the binary logic used in modern computer science.| Attribute | Details |
| Name | Pingala (c. 3rd or 2nd Century BCE) |
| Title | Author of the Chandaḥśāstra |
| Field | Mathematics, Prosody, Linguistics |
| Key Discovery | Binary Number System, Meru Prastara (Pascal’s Triangle) |
| Legacy | Foundations of Combinatorics and Computer Science |
The Rhythm of Logic: Pingala’s Mathematical Poetry
In the ancient halls of Indian scholarship, where the sound of chanting filled the air, a mathematician named Pingala was looking at poetry in a way no one else ever had. While others listened to the beauty of the verses, Pingala was interested in their structure. Through the development of the Pingala Binary System, he transformed the rhythmic patterns of short (Laghu) and long (Guru) syllables into a sophisticated mathematical language. It is a mystery that continues to baffle modern scientists: how did a man living over two thousand years ago create the very logic that runs our smartphones today?
Pingala’s journey began with the Chandaḥśāstra, the earliest known text on Sanskrit prosody. He wasn’t just categorizing poems; he was looking for a way to map out every possible combination of rhythm. To do this, he needed a system of counting that used only two states. In modern times, we call this “0 and 1,” but Pingala used the sounds of language itself to build his binary code. This was not just a linguistic exercise—it was the birth of combinatorics.
8 Defining Chapters in the Vikram Sarabhai Biography
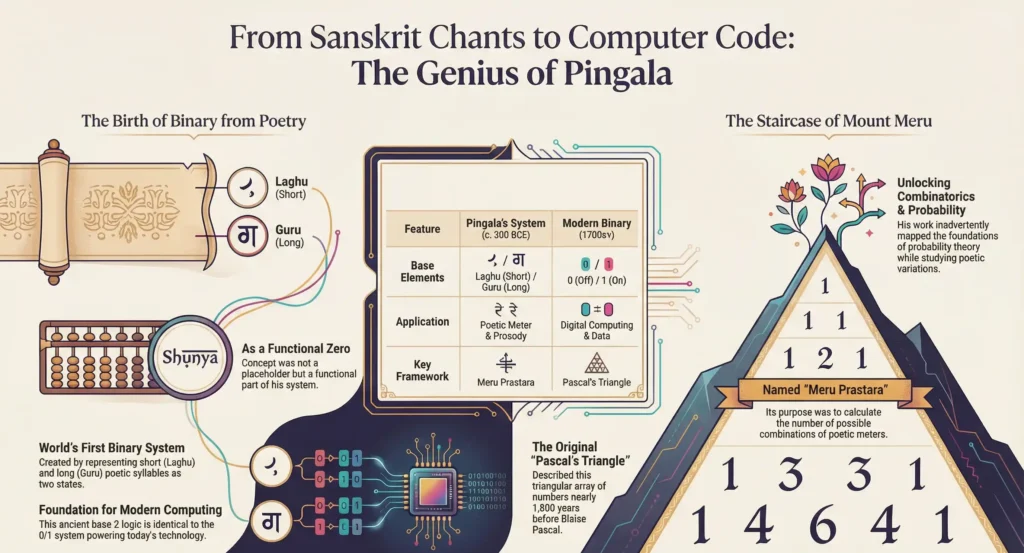
The Mystery of the Meru Prastara
One of the most profound secrets hidden within Pingala’s work is the Meru Prastara, often referred to as the “Staircase of Mount Meru.” For centuries, Western mathematics credited the famous triangle of numbers to Blaise Pascal. However, Pingala had described the exact same triangular array of binomial coefficients nearly 1,800 years earlier.
The mystery lies in his intent. Pingala wasn’t trying to solve an abstract math problem; he was trying to help poets understand how many ways they could arrange a specific number of syllables. By calculating these variations, he inadvertently mapped out the foundations of probability and algebra. For any “Curious Indian,” realizing that the core of Western mathematics has its roots in ancient Indian poetic theory is an inspirational revelation.
From Sanskrit Chants to Computer Code
The Pingala Binary System is remarkably similar to the logic used in modern computing. He used a method called Pratyaya to convert poetic meters into numbers and vice versa. His “shunya” (zero) wasn’t just a placeholder; it was a functional part of a mathematical system that could represent any value using a base-2 structure.
When we look at the history of science, we often see a divide between the arts and the sciences. Pingala bridged this gap with ease. He showed that the music of the human voice and the logic of the universe are one and the same. His life was a testament to the idea that deep observation of nature—even the nature of our own speech—can lead to the discovery of universal truths.
6 Unfoldings in the Subrahmanyan Chandrasekhar Biography
A Legacy Encoded in Time
Despite his massive contribution, Pingala remains a somewhat enigmatic figure. Some traditions link him to the great grammarian Panini, perhaps as a younger brother. This connection suggests a family of geniuses dedicated to the “science of language.” Pingala’s work traveled through the centuries, influencing later Indian mathematicians like Halayudha and Bhaskara, eventually trickling into the global consciousness.
His story is an emotional one for those who value the intellectual history of India. It tells us that we were never “behind” in science; rather, we were so far ahead that we were using the logic of the future to write the poetry of the past. Pingala invites every “Curious Indian” to look at the world with a sense of wonder, searching for the patterns that connect the ancient and the modern.
Quick Comparison: Ancient vs. Modern Logic
| Feature | Pingala’s System (300 BCE) | Modern Binary (1700s+) |
| Base Elements | Laghu (Short) / Guru (Long) | 0 (Off) / 1 (On) |
| Application | Poetic Meter & Prosody | Digital Computing & Data |
| Key Framework | Meru Prastara | Pascal’s Triangle |
| Notation | Written in Sanskrit Sutras | Positional Notation |
| Purpose | To map all possible rhythmic combinations | To represent all numerical/logical data |
Curious Indian: Fast Facts
- The Brother of Panini: Ancient tradition suggests Pingala may have been the brother of Panini, the world’s greatest linguist.
- The First Zero: While the digit “0” is often credited later, Pingala used the concept of Shunya (Zero) in his binary calculations.
- Mount Meru Connection: He called his numerical triangle “Meru Prastara,” comparing its structure to the sacred Himalayan peak.
- Fibonacci Roots: His work on light and heavy syllables also contained the seeds of the Fibonacci sequence long before Fibonacci lived.
- The Art of Memory: Pingala wrote his complex math in short, easy-to-memorize verses called Sutras.
7 Untold Stories of Battle of Asal Uttar 1965 Victory
Conclusion
The genius of the Pingala Binary System proves that ancient India was a powerhouse of mathematical innovation. Pingala didn’t just study poetry; he decoded the very language of existence. His legacy is found in every line of code written today and every digital screen we touch. As we celebrate his life, we are reminded that our history is not just about kings and wars, but about the quiet brilliance of scholars who saw the logic in the rhythm of life. For the “Curious Indian,” Pingala is a symbol of how deep roots in tradition can lead to the most modern of discoveries.
If you think you have remembered everything about this topic take this QUIZ
Results
#1. What is the name of Pingala’s foundational text, which is considered the earliest known work on Sanskrit prosody?
#2. In Pingala’s binary system, which two linguistic elements were used to represent the different mathematical states?
#3. What is the ‘Meru Prastara,’ described by Pingala, known as in modern Western mathematics?
#4. Pingala used a specific concept to represent a functional part of his base-2 mathematical structure. What was it?
#5. Pingala’s work on mapping all possible rhythmic combinations in poetry provided the essential groundwork for which mathematical field?
#6. According to ancient tradition, Pingala is often believed to be the brother of which famous grammarian?
#7. What mathematical sequence, often credited to a 13th-century Italian, has its ‘seeds’ in Pingala’s work on syllables?
#8. How did Pingala record his complex mathematical and linguistic findings to ensure they were easily remembered?
Dr. A.P.J. Abdul Kalam: (1931-2015)
Is Pingala really the inventor of binary code?
Yes, his Chandaḥśāstra contains the first known description of a binary system, used to categorize the meters of Vedic poetry.
How did Pingala use “zero” in his math?
Pingala used the term Shunya specifically in his rules for converting binary combinations into decimal values, marking a critical step in the history of the number zero.
What is the link between Pingala and computer science?
Modern computers operate on binary logic (0 and 1). Pingala’s system of Laghu and Guru syllables is the earliest recorded instance of this two-state logical framework.
What is the Meru Prastara?
It is a triangular arrangement of numbers where each number is the sum of the two above it. Today it is known as Pascal’s Triangle, but Pingala described it centuries earlier.
Why is Pingala’s work considered “prosody”?
Prosody is the study of poetic rhythm. Pingala realized that rhythm is purely mathematical, and by studying it, he discovered deep laws of mathematics.
Read More: https://curiousindian.in/varahamihira-6th-century-ce/








